Momentum of a Particle

Momentum of a Particle#

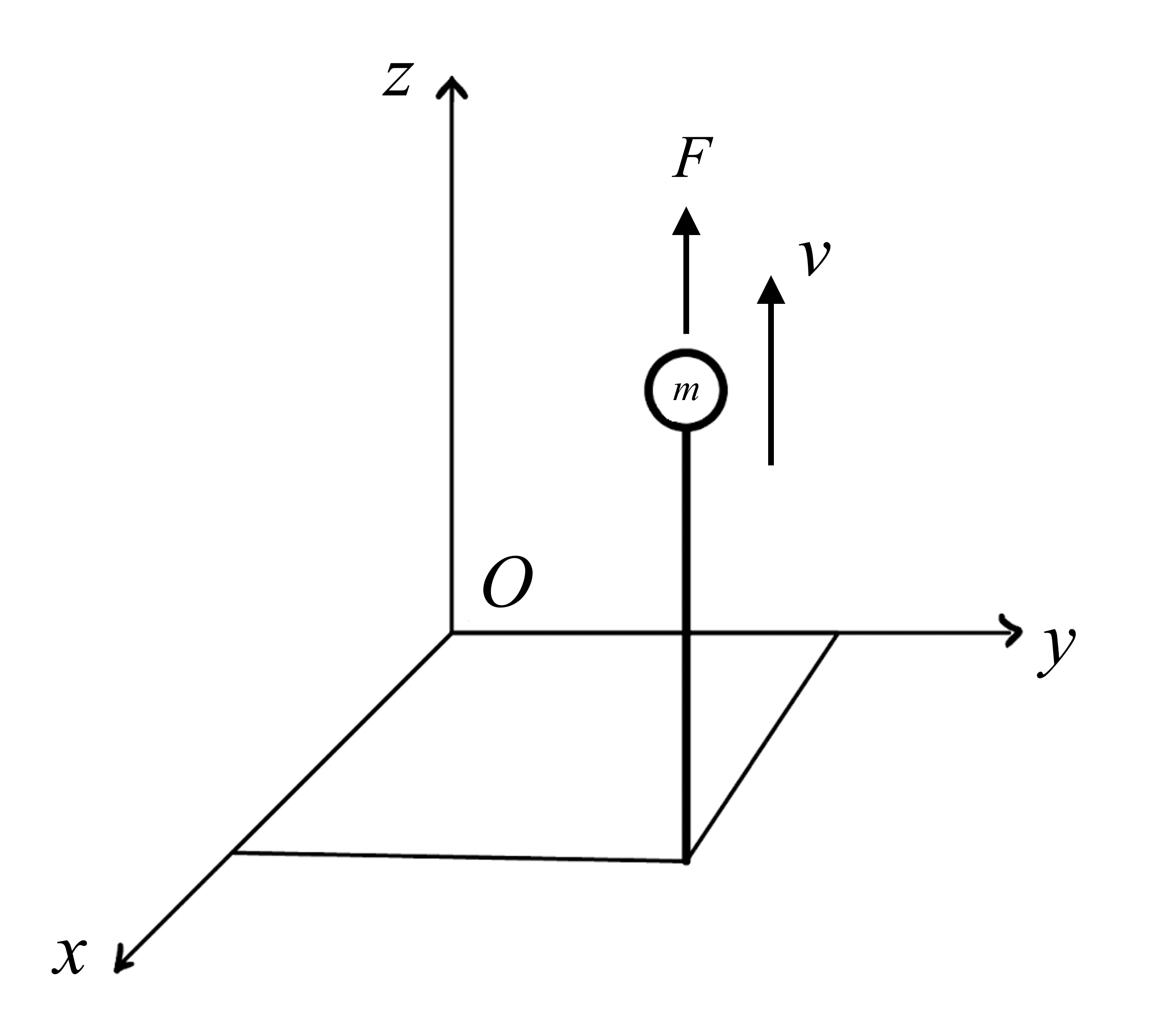
../../../../../_images/Momentum.png

A particle has a mass of \(m = {{params.m}} \ \rm{kg}\) and has a velocity of \(v = {{params.v}} \ \rm{m/s}\). The force acting upon this particle is \(F = {{params.F}} \ \rm{N}\), and the position is given by \(({{params.x}} ,{{params.y}} ,{{params.z}} )\). What is the angular momentum about the origin and its time derivative?

Part 1#

What is \(H_x\)?

Answer Section#

Please enter in a numeric value in \(\rm{N-m-s}\).

Part 2#

What is \(H_y\)?

Answer Section#

Please enter in a numeric value in \(\rm{N-m-s}\).

Part 3#

What is \(H_z\)?

Answer Section#

Please enter in a numeric value in \(\rm{N-m-s}\).

Part 4#

What is \(\dot{H_x}\)?

Answer Section#

Please enter in a numeric value in \(\rm{N.m}\).

Part 5#

What is \(\dot{H_y}\)?

Answer Section#

Please enter in a numeric value in \(\rm{N.m}\).

Part 6#

What is \(\dot{H_z}\)?

Answer Section#

Please enter in a numeric value in \(\rm{N.m}\).

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.